Joint probability distribution
In the study of probability, given two random variables X and Y that are defined on the same probability space, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y. In the case of only two random variables, this is called a bivariate distribution, but the concept generalizes to any number of random variables, giving a multivariate distribution. the equation for joint probability is different for both dependent and independent events.
Contents |
Example
Consider the roll of a die and let  if the number is even (i.e. 2,4, or 6) and
if the number is even (i.e. 2,4, or 6) and 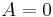 otherwise. Furthermore, let
otherwise. Furthermore, let  if the number is prime (i.e. 2,3, or 5) and
if the number is prime (i.e. 2,3, or 5) and 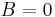 otherwise. Then, the joint distribution of
otherwise. Then, the joint distribution of  and
and  is
is
Cumulative distribution
The cumulative distribution function for a pair of random variables is defined in terms of their joint probability distribution;
Discrete case
The joint probability mass function of two discrete random variables is equal to
In general, the joint probability distribution of  discrete random variables
discrete random variables  is equal to
is equal to
This identity is known as the chain rule of probability.
Since these are probabilities, we have
Continuous case
Similarly for continuous random variables, the joint probability density function can be written as fX,Y(x, y) and this is
where fY|X(y|x) and fX|Y(x|y) give the conditional distributions of Y given X = x and of X given Y = y respectively, and fX(x) and fY(y) give the marginal distributions for X and Y respectively.
Again, since these are probability distributions, one has
Mixed case
In some situations X is continuous but Y is discrete. For example, in a logistic regression, one may wish to predict the probability of a binary outcome Y conditional on the value of a continuously-distributed X. In this case, (X, Y) has neither a probability density function nor a probability mass function in the sense of the terms given above. On the other hand, a "mixed joint density" can be defined in either of two ways:
Formally, fX,Y(x, y) is the probability density function of (X, Y) with respect to the product measure on the respective supports of X and Y. Either of these two decompositions can then be used to recover the joint cumulative distribution function:
The definition generalizes to a mixture of arbitrary numbers of discrete and continuous random variables.
General multidimensional distributions
The cumulative distribution function for a vector of random variables is defined in terms of their joint probability distribution;
The joint distribution for two random variables can be extended to many random variables X1, ... Xn by adding them sequentially with the identity
where
and
(notice, that these latter identities can be useful to generate a random variable  with given distribution function
with given distribution function  ); the density of the marginal distribution is
); the density of the marginal distribution is
The joint cumulative distribution function is
and the conditional distribution function is accordingly
Expectation reads
suppose that h is smooth enough and  for
for  , then, by iterated integration by parts,
, then, by iterated integration by parts,
Joint distribution for independent variables
If for discrete random variables  for all x and y, or for absolutely continuous random variables
for all x and y, or for absolutely continuous random variables  for all x and y, then X and Y are said to be independent.
for all x and y, then X and Y are said to be independent.
Joint Distribution for conditionally independent variables
If a subset  of the variables
of the variables  is conditionally independent given another subset
is conditionally independent given another subset  of these variables, then the joint distribution
of these variables, then the joint distribution  is equal to
is equal to  . Therefore, it can be efficiently represented by the lower-dimensional probability distributions
. Therefore, it can be efficiently represented by the lower-dimensional probability distributions 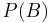 and
and 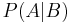 . Such conditional independence relations can be represented with a Bayesian network.
. Such conditional independence relations can be represented with a Bayesian network.
See also
- Chow-Liu tree
- Conditional probability
- Copula (statistics)
- Disintegration theorem
- Multivariate statistics
- Multivariate normal distribution
- Multivariate stable distribution
- Negative multinomial distribution
- Statistical interference









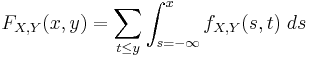







![\mathbb{E}\left[h(X_1,\dots X_n) \right]=\int_{-\infty}^\infty \dots \int_{-\infty}^\infty h(x_1,\dots x_n) f_{X_1,\dots X_n}(x_1,\dots x_n) \mathrm{d} x_1 \dots \mathrm{d} x_n;](/2012-wikipedia_en_all_nopic_01_2012/I/291ca6caee24806f2e7905082f14dec4.png)
![\begin{align}\mathbb{E}\left[h(X_1,\dots X_n) \right]=& h(x_1,\dots x_n)%2B \\
& (-1)^n \int_{-\infty}^{x_1} \dots \int_{-\infty}^{x_n} F_{X_1,\dots X_n}(u_1,\dots u_n) \frac{\partial^n}{\partial x_1 \dots \partial x_n} h(u_1,\dots u_n) \mathrm{d} u_1 \dots \mathrm{d} u_n.\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/3a24fab2c5766d7b38db2b99ecec2e4c.png)